Find the in-order successor of a given node in a binary search tree

Note:

We can do in-order traversal, which will give us a sorted array and then find the in-order successor very easily.

But the time complexity of in-order traversal in O(n).

Where as finding the in-order successor is very frequently used operation. Hence, we need to find better solution.

We will show the solution which will run in O(log(n)).

We will assume the BST is constructed in a way that each node has a reference to its parent.

Case I : Node has a right subtree

In that case we need to find the left most node in its right subtree which is also the min (lowest) node in its right subtree.

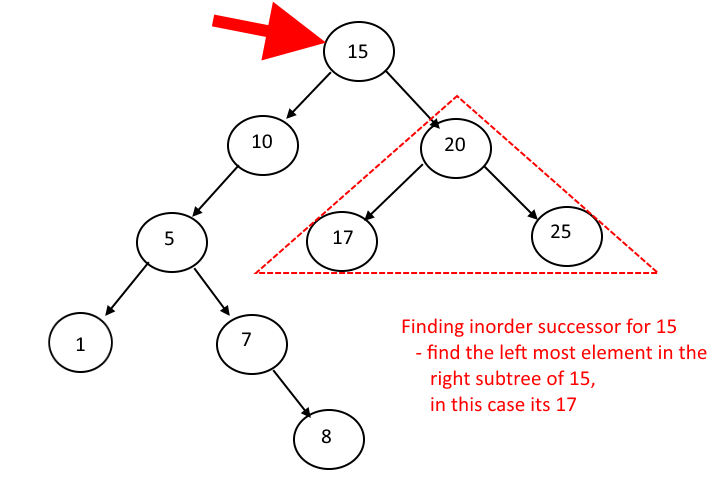
Case II : Node does not have a right subtree

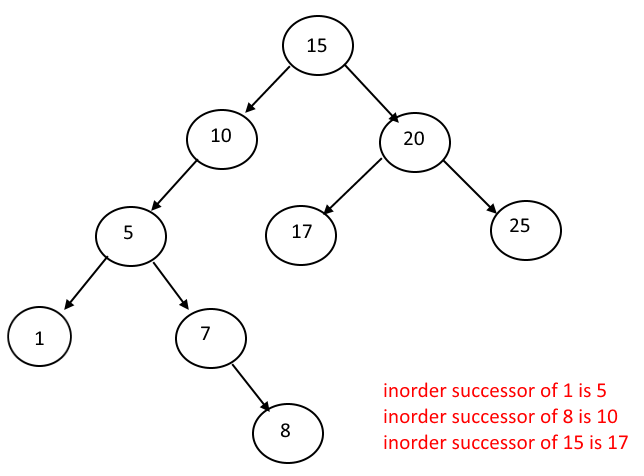
Pseudo code

inorderSuccessor (node n) {

  if (n has a right subtree) {
    return leftmost child of right subtree;
  } else {
    while (n is a right child of n.parent) {
      n = n.parent; // Climb up 
    }
    return n.parent; // Deepest ancestor in the path from root, for which the node would be in the left sub-tree
  }
}

Watch the following excellent video to understand this algorithm in more detail!

Solution

If we have a BST in which each node has a reference to its parent node then the following solution can give us the inOrderSuccessor of the given node.

	'use strict';

	function inOrderSuccessor(node) {
	if (!node) {
	return null;
	}

	if (node.right) {
	return leftMostChild(node.right);
	} else {
	var currentNode = node;
	// Assuming each node has a reference to its parent
	var parentNode = currentNode.parent;

	// Go up until we find deepest ancestor for which node would be in left sub tree
	while (parentNode && parentNode.left !== currentNode) {
	currentNode = parentNode;
	parentNode = parentNode.parent;
	}

	return parentNode;
	}
	}

	function leftMostChild(node) {
	if (!node) {
	return null;
	}
	while (node.left) {
	node = node.left;
	}
	return node;
	}

view raw inOrderSuccessor.js hosted with ❤ by GitHub

CTCI_6_4.6

binary-search-tree 8 cracking the coding interview 5