|
Be the first user to complete this post
|
Add to List |
310. Dijkstra’s – Shortest Path Algorithm (SPT) – Adjacency List and Min Heap
Earlier we have seen the basics of Dijkstra algorithm. In this article, we will see its implementation using the adjacency list and Min Heap.
brief: What is Dijkstra’s algorithm?
- Dijkstra algorithm is a greedy algorithm.
- It finds a shortest path tree for a weighted undirected graph.
- This means it finds the shortest paths between nodes in a graph, which may represent, for example, road networks
- For a given source node in the graph, the algorithm finds the shortest path between the source node and every other node.
- This algorithm is also used for finding the shortest paths from a single node to a single destination node by stopping the algorithm once the shortest path to the destination node has been determined.
- Dijkstra’s algorithm is very similar to Prim’s algorithm. In Prim’s algorithm, we create minimum spanning tree (MST) and in the Dijkstra algorithm, we create a shortest-path tree (SPT) from the given source.
We strongly recommend reading the following articles
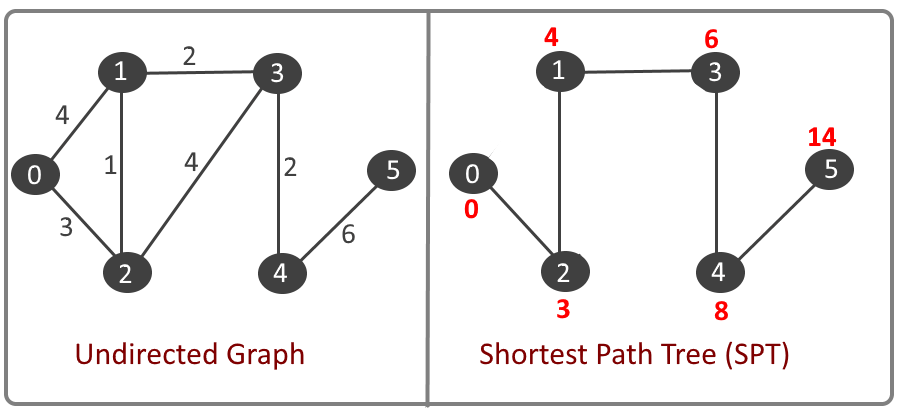
Example:
Implementation – Adjacency List and Min Heap
- Create min Heap of size = no of vertices.
- Create a heapNode for each vertex which will store two pieces of information. a). vertex b). Distance from vertex from source vertex.
- Use spt[] to keep track of the vertices which are currently in min-heap.
- For each heapNode, initialize distance as +∞ except the heapNode for the source vertex for which distance will be 0.
- while minHeap is not empty
- Extract the min node from the heap, say it vertex u, and add it to the SPT.
- Decrease distance: For adjacent vertex v, if v is not in SPT[] and distance[v] > distance[u] + edge u-v weight then update distance[v] = distance[u] + edge u-v weight
Time Complexity:
Total vertices: V, Total Edges : E
- O(logV) – to extract each vertex from the heap. So for V vertices – O(VlogV)
- O(logV) – each time decreases the distance of a vertex. Decrease distance will be called for at most once for each edge. So for total E edge – O(ElogV)
- So overall complexity: O(VlogV) + O(ElogV) = O((E+V)logV) = O(ElogV)
See the animation below for more understanding
Complete Code:
import java.util.LinkedList;
public class Main {
static class Edge {
int source;
int destination;
int weight;
public Edge(int source, int destination, int weight) {
this.source = source;
this.destination = destination;
this.weight = weight;
}
}
static class HeapNode{
int vertex;
int distance;
}
static class Graph {
int vertices;
LinkedList<Edge>[] adjacencylist;
Graph(int vertices) {
this.vertices = vertices;
adjacencylist = new LinkedList[vertices];
//initialize adjacency lists for all the vertices
for (int i = 0; i <vertices ; i++) {
adjacencylist[i] = new LinkedList<>();
}
}
public void addEdge(int source, int destination, int weight) {
Edge edge = new Edge(source, destination, weight);
adjacencylist[source].addFirst(edge);
edge = new Edge(destination, source, weight);
adjacencylist[destination].addFirst(edge); //for undirected graph
}
public void dijkstra_GetMinDistances(int sourceVertex){
int INFINITY = Integer.MAX_VALUE;
boolean[] SPT = new boolean[vertices];
// //create heapNode for all the vertices
HeapNode [] heapNodes = new HeapNode[vertices];
for (int i = 0; i <vertices ; i++) {
heapNodes[i] = new HeapNode();
heapNodes[i].vertex = i;
heapNodes[i].distance = INFINITY;
}
//decrease the distance for the first index
heapNodes[sourceVertex].distance = 0;
//add all the vertices to the MinHeap
MinHeap minHeap = new MinHeap(vertices);
for (int i = 0; i <vertices ; i++) {
minHeap.insert(heapNodes[i]);
}
//while minHeap is not empty
while(!minHeap.isEmpty()){
//extract the min
HeapNode extractedNode = minHeap.extractMin();
//extracted vertex
int extractedVertex = extractedNode.vertex;
SPT[extractedVertex] = true;
//iterate through all the adjacent vertices
LinkedList<Edge> list = adjacencylist[extractedVertex];
for (int i = 0; i <list.size() ; i++) {
Edge edge = list.get(i);
int destination = edge.destination;
//only if destination vertex is not present in SPT
if(SPT[destination]==false ) {
///check if distance needs an update or not
//means check total weight from source to vertex_V is less than
//the current distance value, if yes then update the distance
int newKey = heapNodes[extractedVertex].distance + edge.weight ;
int currentKey = heapNodes[destination].distance;
if(currentKey>newKey){
decreaseKey(minHeap, newKey, destination);
heapNodes[destination].distance = newKey;
}
}
}
}
//print SPT
printDijkstra(heapNodes, sourceVertex);
}
public void decreaseKey(MinHeap minHeap, int newKey, int vertex){
//get the index which distance's needs a decrease;
int index = minHeap.indexes[vertex];
//get the node and update its value
HeapNode node = minHeap.mH[index];
node.distance = newKey;
minHeap.bubbleUp(index);
}
public void printDijkstra(HeapNode[] resultSet, int sourceVertex){
System.out.println("Dijkstra Algorithm: (Adjacency List + Min Heap)");
for (int i = 0; i <vertices ; i++) {
System.out.println("Source Vertex: " + sourceVertex + " to vertex " + + i +
" distance: " + resultSet[i].distance);
}
}
}
static class MinHeap{
int capacity;
int currentSize;
HeapNode[] mH;
int [] indexes; //will be used to decrease the distance
public MinHeap(int capacity) {
this.capacity = capacity;
mH = new HeapNode[capacity + 1];
indexes = new int[capacity];
mH[0] = new HeapNode();
mH[0].distance = Integer.MIN_VALUE;
mH[0].vertex=-1;
currentSize = 0;
}
public void display() {
for (int i = 0; i <=currentSize; i++) {
System.out.println(" " + mH[i].vertex + " distance " + mH[i].distance);
}
System.out.println("________________________");
}
public void insert(HeapNode x) {
currentSize++;
int idx = currentSize;
mH[idx] = x;
indexes[x.vertex] = idx;
bubbleUp(idx);
}
public void bubbleUp(int pos) {
int parentIdx = pos/2;
int currentIdx = pos;
while (currentIdx > 0 && mH[parentIdx].distance > mH[currentIdx].distance) {
HeapNode currentNode = mH[currentIdx];
HeapNode parentNode = mH[parentIdx];
//swap the positions
indexes[currentNode.vertex] = parentIdx;
indexes[parentNode.vertex] = currentIdx;
swap(currentIdx,parentIdx);
currentIdx = parentIdx;
parentIdx = parentIdx/2;
}
}
public HeapNode extractMin() {
HeapNode min = mH[1];
HeapNode lastNode = mH[currentSize];
// update the indexes[] and move the last node to the top
indexes[lastNode.vertex] = 1;
mH[1] = lastNode;
mH[currentSize] = null;
sinkDown(1);
currentSize--;
return min;
}
public void sinkDown(int k) {
int smallest = k;
int leftChildIdx = 2 * k;
int rightChildIdx = 2 * k+1;
if (leftChildIdx < heapSize() && mH[smallest].distance > mH[leftChildIdx].distance) {
smallest = leftChildIdx;
}
if (rightChildIdx < heapSize() && mH[smallest].distance > mH[rightChildIdx].distance) {
smallest = rightChildIdx;
}
if (smallest != k) {
HeapNode smallestNode = mH[smallest];
HeapNode kNode = mH[k];
//swap the positions
indexes[smallestNode.vertex] = k;
indexes[kNode.vertex] = smallest;
swap(k, smallest);
sinkDown(smallest);
}
}
public void swap(int a, int b) {
HeapNode temp = mH[a];
mH[a] = mH[b];
mH[b] = temp;
}
public boolean isEmpty() {
return currentSize == 0;
}
public int heapSize(){
return currentSize;
}
}
public static void main(String[] args) {
int vertices = 6;
Graph graph = new Graph(vertices);
int sourceVertex = 0;
graph.addEdge(0, 1, 4);
graph.addEdge(0, 2, 3);
graph.addEdge(1, 2, 1);
graph.addEdge(1, 3, 2);
graph.addEdge(2, 3, 4);
graph.addEdge(3, 4, 2);
graph.addEdge(4, 5, 6);
graph.dijkstra_GetMinDistances(sourceVertex);
}
}
import heapq
class Graph:
class Edge:
def __init__(self, source, destination, weight):
self.source = source
self.destination = destination
self.weight = weight
class HeapNode:
def __init__(self, vertex, distance):
self.vertex = vertex
self.distance = distance
def __lt__(self, other):
return self.distance < other.distance
def __init__(self, vertices):
self.vertices = vertices
self.adjacencylist = [[] for _ in range(vertices)]
def add_edge(self, source, destination, weight):
edge = self.Edge(source, destination, weight)
self.adjacencylist[source].append(edge)
edge = self.Edge(destination, source, weight)
self.adjacencylist[destination].append(edge)
def dijkstra_get_min_distances(self, source_vertex):
INFINITY = float('inf')
spt = [False] * self.vertices
# create heapNode for all the vertices
heap_nodes = [self.HeapNode(i, INFINITY) for i in range(self.vertices)]
# decrease the distance for the first index
heap_nodes[source_vertex].distance = 0
# add all the vertices to the MinHeap
min_heap = []
heapq.heapify(min_heap)
for heap_node in heap_nodes:
heapq.heappush(min_heap, heap_node)
# while MinHeap is not empty
while min_heap:
# extract the min
extracted_node = heapq.heappop(min_heap)
# extracted vertex
extracted_vertex = extracted_node.vertex
spt[extracted_vertex] = True
# iterate through all the adjacent vertices
for edge in self.adjacencylist[extracted_vertex]:
destination = edge.destination
# only if destination vertex is not present in SPT
if not spt[destination]:
# check if distance needs an update or not
# means check if the total weight from source to vertex_V is less than
# the current distance value, if yes then update the distance
new_key = extracted_node.distance + edge.weight
current_key = heap_nodes[destination].distance
if current_key > new_key:
self.decrease_key(min_heap, new_key, destination)
heap_nodes[destination].distance = new_key
# print SPT
self.print_dijkstra(heap_nodes, source_vertex)
@staticmethod
def decrease_key(min_heap, new_key, vertex):
# get the index which distance needs a decrease
for i, heap_node in enumerate(min_heap):
if heap_node.vertex == vertex:
min_heap[i].distance = new_key
heapq.heapify(min_heap)
return
@staticmethod
def print_dijkstra(result_set, source_vertex):
print("Dijkstra Algorithm: (Adjacency List + Min Heap)")
for i in range(len(result_set)):
print(f"Source Vertex: {source_vertex} to vertex {i} distance: {result_set[i].distance}")
def main():
vertices = 6
graph = Graph(vertices)
source_vertex = 0
graph.add_edge(0, 1, 4)
graph.add_edge(0, 2, 3)
graph.add_edge(1, 2, 1)
graph.add_edge(1, 3, 2)
graph.add_edge(2, 3, 4)
graph.add_edge(3, 4, 2)
graph.add_edge(4, 5, 6)
graph.dijkstra_get_min_distances(source_vertex)
if __name__ == "__main__":
main()
package main
import (
"container/heap"
"fmt"
"math"
)
type Edge struct {
source int
destination int
weight int
}
type HeapNode struct {
vertex int
distance int
}
type MinHeap []HeapNode
func (h MinHeap) Len() int { return len(h) }
func (h MinHeap) Less(i, j int) bool { return h[i].distance < h[j].distance }
func (h MinHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *MinHeap) Push(x interface{}) {
*h = append(*h, x.(HeapNode))
}
func (h *MinHeap) Pop() interface{} {
old := *h
n := len(old)
x := old[n-1]
*h = old[0 : n-1]
return x
}
type Graph struct {
vertices int
adjacencylist map[int][]Edge
}
func newGraph(vertices int) *Graph {
return &Graph{
vertices: vertices,
adjacencylist: make(map[int][]Edge),
}
}
func (g *Graph) addEdge(source, destination, weight int) {
edge := Edge{
source: source,
destination: destination,
weight: weight,
}
g.adjacencylist[source] = append(g.adjacencylist[source], edge)
g.adjacencylist[destination] = append(g.adjacencylist[destination], Edge{
source: destination,
destination: source,
weight: weight,
})
}
func dijkstra(graph *Graph, sourceVertex int) []int {
INFINITY := int(^uint(0) >> 1)
distance := make([]int, graph.vertices)
visited := make([]bool, graph.vertices)
for i := 0; i < graph.vertices; i++ {
distance[i] = INFINITY
visited[i] = false
}
distance[sourceVertex] = 0
minHeap := &MinHeap{{sourceVertex, 0}}
heap.Init(minHeap)
for minHeap.Len() > 0 {
u := heap.Pop(minHeap).(HeapNode).vertex
visited[u] = true
for _, edge := range graph.adjacencylist[u] {
v := edge.destination
if !visited[v] {
newDistance := distance[u] + edge.weight
if newDistance < distance[v] {
distance[v] = newDistance
heap.Push(minHeap, HeapNode{vertex: v, distance: newDistance})
}
}
}
}
return distance
}
func main() {
vertices := 6
graph := newGraph(vertices)
sourceVertex := 0
graph.addEdge(0, 1, 4)
graph.addEdge(0, 2, 3)
graph.addEdge(1, 2, 1)
graph.addEdge(1, 3, 2)
graph.addEdge(2, 3, 4)
graph.addEdge(3, 4, 2)
graph.addEdge(4, 5, 6)
distances := dijkstra(graph, sourceVertex)
fmt.Println("Dijkstra Algorithm:")
for i, distance := range distances {
fmt.Println("Source Vertex:", sourceVertex, "to vertex", i, "distance:", distance)
}
}Output:
Dijkstra Algorithm: (Adjacency List + Min Heap) Source Vertex: 0 to vertex 0 distance: 0 Source Vertex: 0 to vertex 1 distance: 4 Source Vertex: 0 to vertex 2 distance: 3 Source Vertex: 0 to vertex 3 distance: 6 Source Vertex: 0 to vertex 4 distance: 8 Source Vertex: 0 to vertex 5 distance: 14