This post is completed by 2 users

  • 1
 Add to List
Medium

168. Dynamic Programming - Minimum Cost Path Problem

Objective: Given a 2D matrix where each cell has a cost to travel. You have to write an algorithm to find a path from the left-top corner to the bottom-right corner with minimum travel cost. You can move only right or down.

In the solution, we will see how dynamic programming is a much better approach than recursion.

Example:

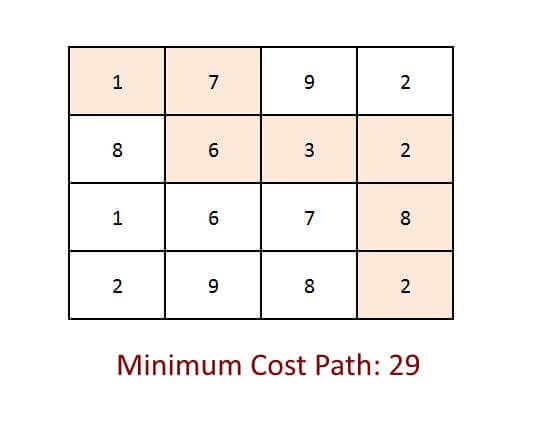
MInimum-Cost-Path-Problem
MInimum-Cost-Path-Problem

Approach:

This problem is similar to Find all paths from top-left corner to bottom-right corner.

We can solve it using Recursion ( return Min(path going right, path going down)) but that won't be a good solution because we will be solving many sub-problems multiple times. Since at every cell we have 2 options the time complexity will be O(2n).

Dynamic Programming:

Create a solution matrix of the same size as a given matrix.

We will fill this matrix in Bottom-up manner.

Given: arrA[][].

At every cell, we have two options (go right or down) and we will choose the minimum of these two.

So for any i,j cell

solution[i][j] = A[0][j] if i=0 , first row

= A[i][0] if j=0, first column

= A[i][j] + Min(solution[i-1],[j] , solution[i][j-1]) if i>0 && j>0

See the code for better Explanation.

Time Complexity: O(n2).

Output

Minimum Cost Path 29

Related Problems: